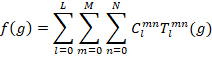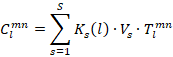Texture measurement is done in most cases by measuring pole figures. A pole figure P_hkl describes the volume fraction dV/V of the crystallites whose crystallographic directions <hkl> have a certain orientation in space: 

dV/V = P_hkl(α, β)·sin α dα dβ

A pole figure is given graphically as a frequency distribution if crystal orientations on the reference sphere that is stereographically projected into the "equator" plane in sample space.  

 

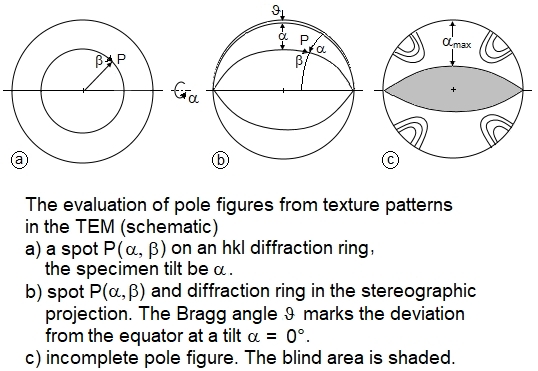
Schematics of a pole figure and its stereographic projection

1. The TEM as an automated texture goniometer

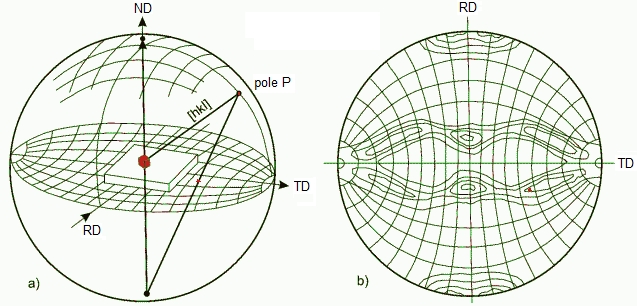
1983	Acquisition of pole figures by post-specimen beam deflection, but manual correction for the ellipticity of diffraction rings.  F.J. Humphreys: Textures and Microstructures 6 (1983) 45-62
1983	Analytical and experimental on-line intensity correction for SAD pole figures in pre- and post-specimen beam deflection mode. R. Schwarzer: Beitr. Elektronenmikr. Direktabb. Oberfl. (BEDO) 16 (1983) 131-134
1984	Automated SAD pole-figure measurement with pre- and post-specimen beam deflection. On-line correction for background, absorption, diffracting volume and ring ellipticity by the software. H. Weiland and R. Schwarzer: Proc. ICOTOM 7 (1984) 857-862 R. Schwarzer: BEDO 18 (1985) 61-68 R.A. Schwarzer and H. Weiland: in H.J. Bunge (ed.): Experimental techniques of texture analysis. DGM Informations-Ges. Oberursel, 1986, 287-300
1998	RHEED pole-figure measurement on bulk surfaces in the TEM. A digital CCD camera is used as an area detector. B. Schäfer and R.A. Schwarzer: Materials Science Forum 273-275 (1998) 223-228
	Features:            + Measured area:  SAD           1 μm .... 500 μm                   RHEED       ~ 0.1 - 2 mm            + High speed: ~ 5 min for the acquisition of several pole figures                        + Extremely high sensitivity.

2. The principles of SAD pole-figure measurement

 

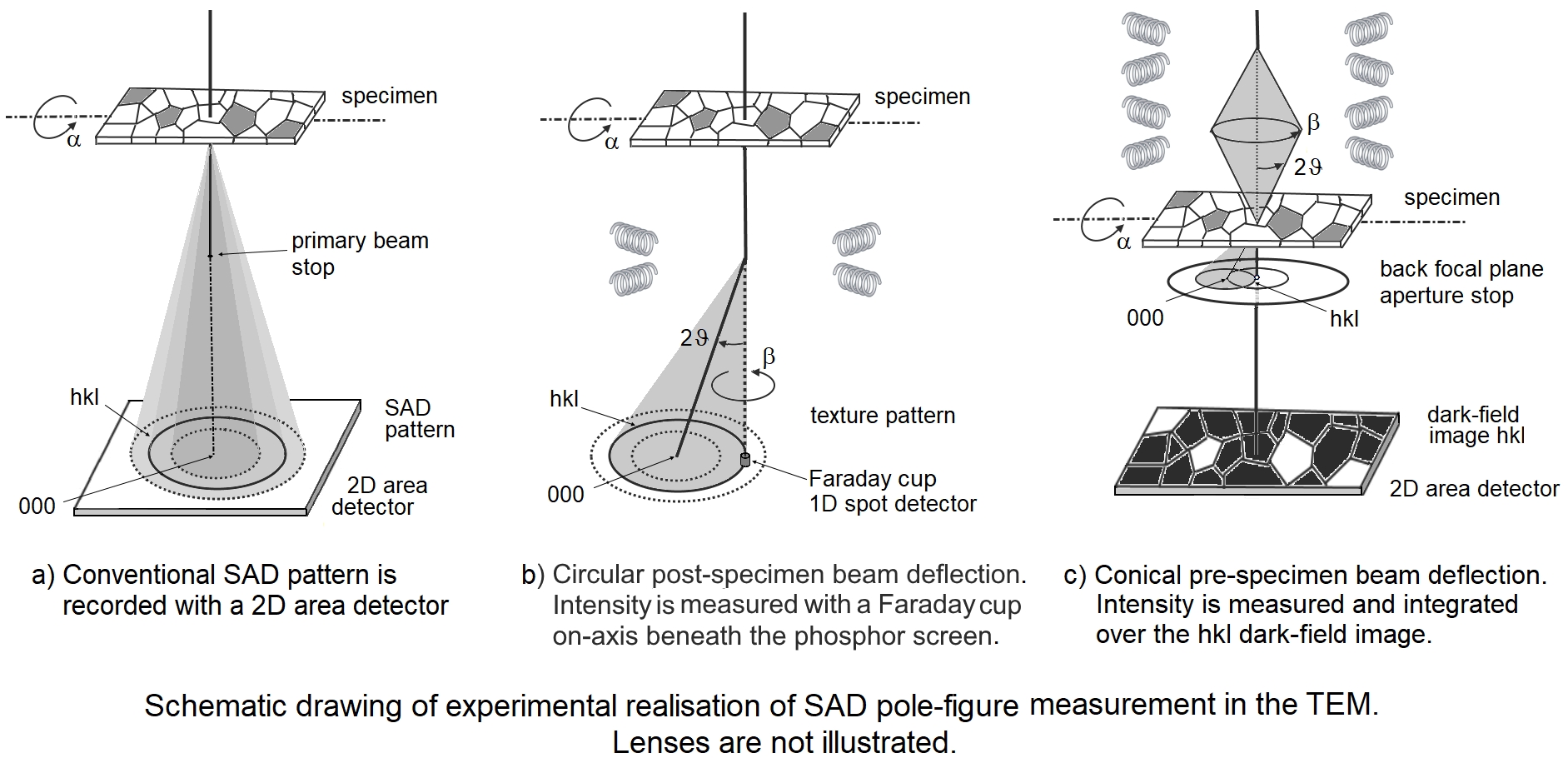
3. The Orientation Density Function ODF

The Orientation Density Function (ODF) and pole figures can be constructed either directly from a data set of individual grain orientations by associating the orientations or the volume fractions of grains having these orientations with points or discrete cells of finite size in the Euler orientation space, on pole figures (stereographic projection) or on inverse pole figures (standard triangle of the crystal symmetry group). Historically, the ODF is calculated by the inversion of pole-figure data from (integral) X-ray diffraction. Various inversion methods have been developed. An elegant approach to smooth and to condense the data set into a continuous representation is the calculation of the ODF, f(g), by series expansion into generalized spherical harmonics (T functions) after Bunge [1]:

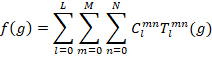
The expansion coefficients (termed "C coefficients") are then expressed by

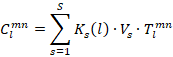
V_s stands for the volume fraction of grain s, and K_s(l) for the convolution kernel of the expansion. Common convolution kernels are a Dirac δ function in case of a large number S of orientations, or Gauss type distributions in Euler space with a half width Ψ_0s at 1/e maximum of the Gauss peak at the orientation point g_s [2, 3]

 

The C coefficients are a highly concise and convenient description of crystal texture. They enable the calculation of normal and inverse pole figures, important elastic and plastic materials properties, and tensorial properties in general [1]. ODFs calculated from EBSD and from X-ray pole figure measurements usually agree very well if the data have been acquired on the same specimen area.

N.B.: In X-ray diffraction, the reflections and hence pole figures are indexed according to their diffracting lattice planes {hkl}. By tradition, inverse pole figures referred to the specimen surface are also indexed according to the in-surface lattice planes rather than to the crystallographic directions perpendicular to the specimen surface. This inconsequent definition is of no relevance in case of cubic crystal symmetry, but has to be kept in mind when studying materials of lower symmetry.

You should keep in mind:
- The ODF is only partially suitable for predicting the properties of engineering materials. The ODF is an idealizing model of the polycrystalline solid that reflects only the volume fraction statistics respectively the numbers of crystal orientations in the measured sample. It completely ignores the stereology of the microstructure, i.e. in particular the location of crystallites, the size of individual grains, their size distribution in the microstructure, their relationship and interaction with their neighborhood, grain boundaries and phase joints, joint properties, and the sub-microstructure (e.g. dislocations, stacking faults and inclusions). The ODF, calculated from the pole figure inversion, is not unique, but depends on the calculation method.
- Amorphous phases are not detected in the pole figure measurement.
- The Eulerian space has a very distorting metric. The ODF representation in Eulerian space therefore easily leads to misinterpretations when considering the usual 3D Cartesian representation. The distortion for pole figures in the usual stereographic projection must also be considered. 
+ From EBSD data, however, the ODF can be constructed unambiguously  by writing the measured volume-weighted or number-weighted orientation of the crystallites, for example in 3D Eulerian space.
+ This ODF can then be compared to the results of current measurements (conventional pole figure measurement by X-ray diffraction, synchrotron or neutron) or to historical measurements from the literature.
+ The ODF in serial development according to Bunge is a very compact summary. When the textures are not too flat, a few development coefficients are often sufficient for useful texture characterization and material property estimation.
_____________
[1] H.-J. Bunge: Texture analysis in materials science - Mathematical methods. Butterworths, London 1982 (ISBN 0-408-10642-5)
Download Paper back reprint: Cuvillier-Verlag Göttingen 1993 ( ISBN 3-928815-81-4)
[2] F. Wagner: Texture determination by individual orientation measurements. In: Experimental Techniques of Texture Analysis, H.J. Bunge (ed.). DGM-Informations-Ges., Oberursel 1986, 115-123 (ISBN 3-88355-101-5)
[3] J. Pospiech: The smoothing of the orientation distribution density introduced by calculation methods. Textures and Microstructures 26-27 (1996) 83-91